Explore Topics

Core Concepts

Heaps

A Heap is a special Tree-based data structure that satisfies the Heap Property.

Types of Heap

A heap is a complete binary tree where elements are arranged based on a specific order. There are different types of heaps:

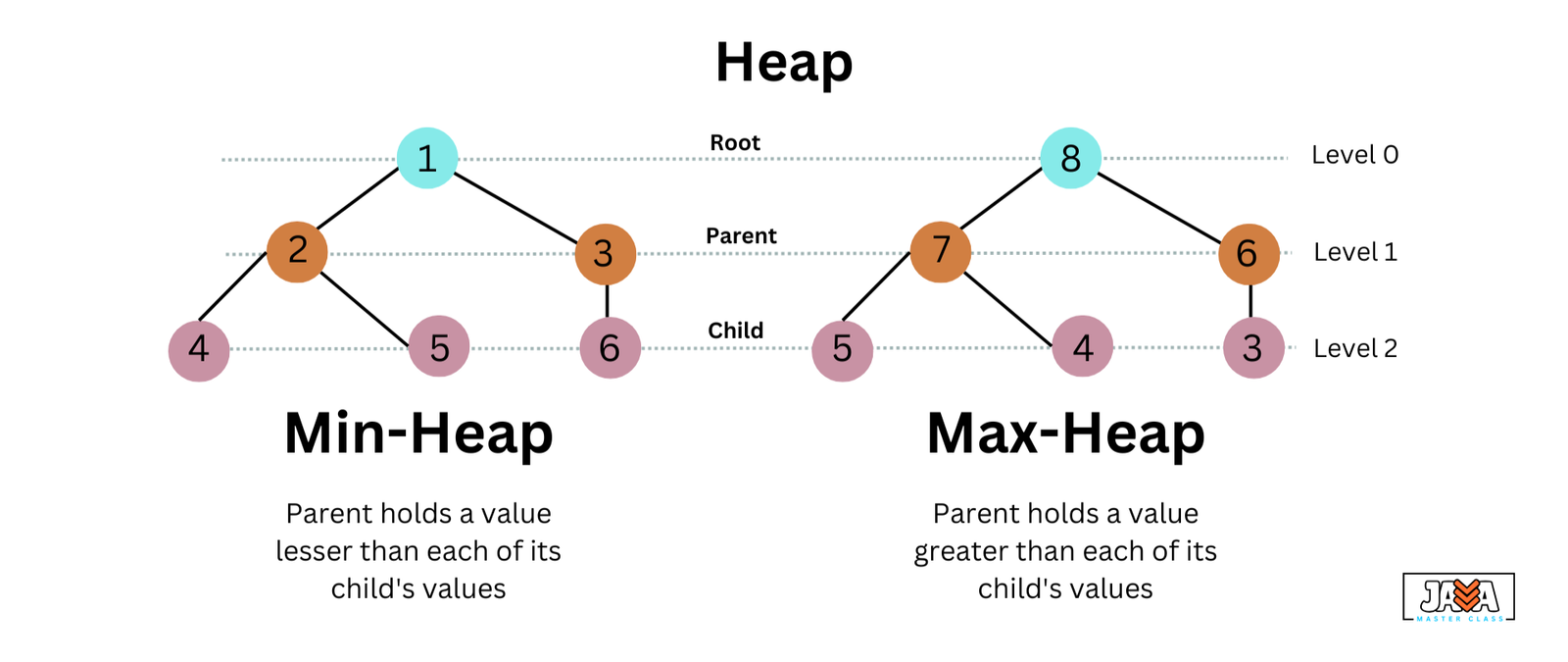
Min-Heap: The parent node is always smaller than its children. The smallest element is at the root.
Max-Heap: The parent node is always larger than its children. The largest element is at the root.
Binary Heap: A complete binary tree following the heap property.
Fibonacci Heap: Advanced heap structure with better amortized time for decrease-key and merge operations, often used in complex graph algorithms.

Declaration & Initialization

In Java, PriorityQueue is the most common class to create heap structures, defaulting to a Min-Heap behavior.

// Min-Heap using PriorityQueue (default behavior)

PriorityQueue<Integer> minHeap = new PriorityQueue<>();

// Max-Heap using PriorityQueue with reverse order comparator

PriorityQueue<Integer> maxHeap = new PriorityQueue<>(Collections.reverseOrder());

Basic Operations

A heap supports three primary operations:

Insertion (add or offer): Adds an element while maintaining the heap property. (O(log N))
Deletion (poll): Removes the root element and reorders the heap. (O(log N))
Peek (peek): Retrieves the root element without removing it. (O(1))

// Insertion (add elements)

minHeap.add(15);

minHeap.add(8);

minHeap.add(25);

// Deletion (poll removes the root, which is the smallest element in Min-Heap)

int min = minHeap.poll(); // removes 8 (smallest)

// Peek (to view the root without removing)

int peekMin = minHeap.peek(); // returns 15

// Traversal (unordered, as heap does not guarantee sorted traversal)

for (int val : minHeap) {

System.out.println(val);

}

Implementation of Heap

Min-Heap Implementation

Java provides a built-in PriorityQueue class that internally uses a min-heap by default.

import java.util.PriorityQueue;

public class HeapExample {

public static void main(String[] args) {

// Creating a Min-Heap

PriorityQueue<Integer> minHeap = new PriorityQueue<>();

// Adding elements

minHeap.add(20);

minHeap.add(10);

minHeap.add(30);

minHeap.add(5);

// Removing elements (smallest first)

while (!minHeap.isEmpty()) {

System.out.println(minHeap.poll()); // Prints elements in sorted order: 5, 10, 20, 30

}

Max-Heap Implementation

import java.util.PriorityQueue;

import java.util.Collections;

public class MaxHeapExample {

public static void main(String[] args) {

// Creating a Max-Heap

PriorityQueue<Integer> maxHeap = new PriorityQueue<>(Collections.reverseOrder());

// Adding elements

maxHeap.add(20);

maxHeap.add(10);

maxHeap.add(30);

maxHeap.add(5);

// Removing elements (largest first)

while (!maxHeap.isEmpty()) {

System.out.println(maxHeap.poll()); // Prints elements in descending order: 30, 20, 10, 5

}

Advantages & Disadvantages

Advantages	Disadvantages
Fast insertion and deletion (O(log n))	Poor performance for arbitrary search (O(n))
Easy to implement using arrays	Doesn’t maintain sorted order during traversal
Ideal for priority-based tasks (Priority Queue)	Can require reheapify after updates

Real World Examples

Priority Queues: For scheduling tasks (OS process scheduling, CPU task management).
Dijkstra’s Shortest Path Algorithm: Min-Heap is used to efficiently pick the next vertex with the smallest distance.
Heap Sort Algorithm: Sorting technique that uses a Max-Heap to repeatedly remove the largest element.
Event simulation systems: Where future events are scheduled based on priority or timestamps.