Trees are a crucial data structure that represent hierarchical relationships. A tree consists of nodes connected by edges. The structure mimics a tree in the real world, where the root node represents the base, and branches extend to various other nodes. Trees are particularly useful for organizing data in a way that allows efficient searching, insertion, and deletion.
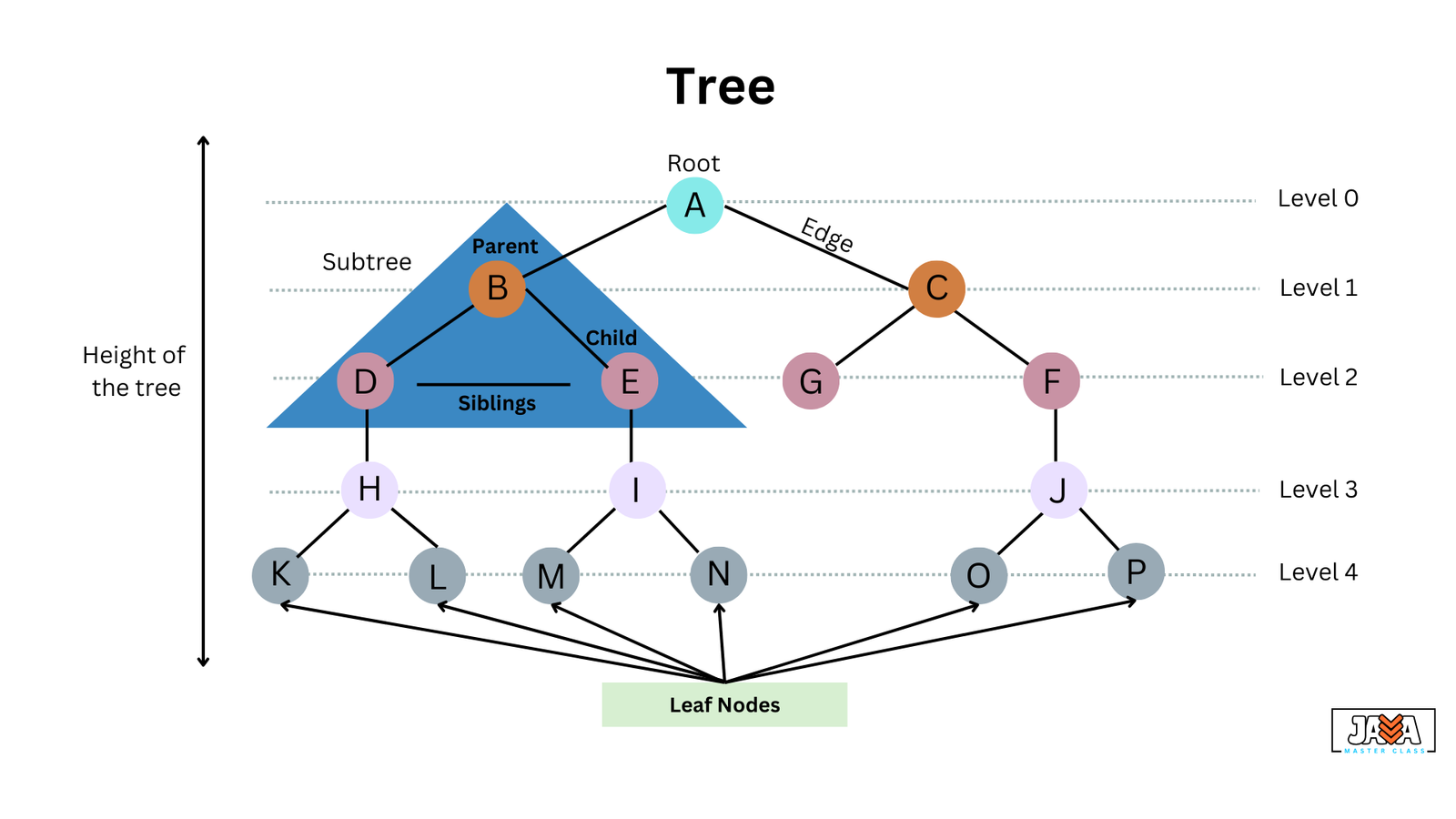
Components of a Tree
- Root: The topmost node in a tree, from which all other nodes descend.
- Node: A fundamental part of a tree that contains data.
- Edge: A connection between two nodes.
- Parent: A node that has one or more child nodes.
- Child: A node that descends from a parent node.
- Leaf: A node with no children, situated at the end of branches.
- Subtree: A tree formed by a node and its descendants.
- Height: The number of edges from a node to the furthest leaf node.
- Depth: The number of edges from the root to the node.
Types of Trees
- Binary Tree: A tree where each node has at most two children (left and right).
- Binary Search Tree (BST): A special type of binary tree where the left child is smaller and the right child is larger than the parent node.
- AVL Tree: A self-balancing binary search tree where the difference in heights between left and right subtrees of any node is at most one.
- Heap: A special tree-based structure that satisfies the heap property (max-heap or min-heap).
- Trie: A tree used to store associative data structures, often used for dictionaries and autocomplete.
Basic Operations
- Insertion: Adding a new node to the tree.
- Traversal: Visiting all the nodes in a particular order. Common traversal methods are:
- Pre-order: Visit the root, then recursively visit the left subtree, followed by the right subtree.
- In-order: Recursively visit the left subtree, then the root, and finally the right subtree.
- Post-order: Recursively visit the left and right subtrees, and then visit the root.
- Level-order: Visit all nodes at the present depth level before moving on to nodes at the next depth level.
- Search: Finding a node with a given value. In binary search trees, this operation can be performed efficiently by leveraging the ordering property of the nodes.
- Deletion: Removing a node from the tree. The complexity depends on whether the node has children, and how many.
Binary Tree Implementation
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 |
class Node { int data; Node left, right; public Node(int item) { data = item; left = right = null; } } class BinaryTree { Node root; // Pre-order traversal void preOrder(Node node) { if (node == null) { return; } System.out.print(node.data + " "); preOrder(node.left); preOrder(node.right); } // In-order traversal void inOrder(Node node) { if (node == null) { return; } inOrder(node.left); System.out.print(node.data + " "); inOrder(node.right); } // Post-order traversal void postOrder(Node node) { if (node == null) { return; } postOrder(node.left); postOrder(node.right); System.out.print(node.data + " "); } // Search for a value in the tree boolean search(Node node, int value) { if (node == null) { return false; } if (node.data == value) { return true; } return search(node.left, value) || search(node.right, value); } public static void main(String[] args) { BinaryTree tree = new BinaryTree(); tree.root = new Node(1); tree.root.left = new Node(2); tree.root.right = new Node(3); tree.root.left.left = new Node(4); tree.root.left.right = new Node(5); System.out.println("Pre-order traversal:"); tree.preOrder(tree.root); System.out.println("\nIn-order traversal:"); tree.inOrder(tree.root); System.out.println("\nPost-order traversal:"); tree.postOrder(tree.root); System.out.println("\nSearch for 4: " + tree.search(tree.root, 4)); System.out.println("Search for 6: " + tree.search(tree.root, 6)); } } |
- Node class: Represents each node in the tree. It contains the
dataof the node and references to its left and right children. - BinaryTree class: Contains methods for pre-order, in-order, and post-order traversal of the tree.
- Search method: Searches for a node with a specific value in the tree.
Output:
|
1 2 3 4 5 6 7 8 |
Pre-order traversal: 1 2 4 5 3 In-order traversal: 4 2 5 1 3 Post-order traversal: 4 5 2 3 1 Search for 4: true Search for 6: false |
Advantages & Disadvantages
| Advantages | Disadvantages |
|---|---|
| Efficient searching, especially in Binary Search Trees (BST). | Can become unbalanced, leading to inefficient operations. |
| Hierarchical representation of data is intuitive. | Traversal and modification can be complex. |
| Supports dynamic memory allocation (no need to predefine size). | Memory overhead due to extra pointers (left, right). |
| Allows for efficient searching, insertion, and deletion. | More complex to implement compared to arrays. |
Real World Examples
- File Systems: Files and directories are represented as a tree structure, where the root is the root directory and subdirectories and files form the children.
- Organization Hierarchy: Company structures can be represented as trees with employees as nodes and managers as parent nodes.
- Autocompletion: Tries are used in search engines and text editors to offer suggestions based on the input prefix.
- Decision Trees: Used in AI for decision-making processes and machine learning algorithms
